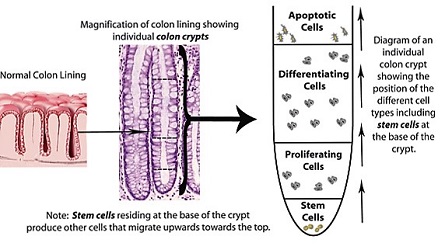The goal of this project is to better understand what causes disruption of normal tissue homeostasis in the colonic epithelium leading to neoplastic tissue changes and loss of function, and ultimately colon cancer. Models being considered are spatial-temporal description of cell population dynamics within normal human colonic crypts (small invaginations in the epithelium). Our models are designed to discover mechanisms that give rise to alterations in tissue dynamics that occur during colon cancer development. This research will also provide a mathematical definition for stem cells and provide an explanation for how stem cell overpopulation occurs in colon cancer and drives tumor growth. The biochemical signals received by the colonic crypt cells are also modeled in order to understand possible disruptions of normal cell behavior and its consequent effect on cell dynamics in the crypt. Understanding cancer in mathematical terms will provide new insights into how to design new more effective, potentially even curative, treatment for patients with advanced cancers. The project involves an integration of biology, mathematics and cancer medicine.

Cardiovascular disease (CVD) is a widespread and expensive medical condition in Western developed nations. Atherosclerotic plaque, which is a manifestation of CVD, is a fatty deposit that lines the interior of large arteries. The growth and subsequent rupture of so-called "vulnerable" plaques account for the majority of myocardial infarctions. The prevention and treatment of atherosclerosis, and heart disease in general, is an outstanding problem in medicine today. Dr Fok's research aims to understand the biological mechanisms behind atherosclerotic plaque growth through mathematical models. Specifically, he is interested in how vessels remodel as they become more diseased, how their dimensions change and how these dimensions are affected by growth factors and vasodilating agents. The main tools he employs are computation, partial differential equations and elasticity theory. More information can be found at Prof. Fok's research page.

This research project is directed towards developing mathematical and computational methods arising from quantitative ultrasound techniques (QUT) for detecting osteoporosis, a major public health threat affecting more than 44 million Americans. Understanding the bio-mechanical advance of the disease and developing quantitative mathematical techniques for its monitoring is the first step towards efficient treatment and prevention. Diagnostics based on QUT is relatively inexpensive and, unlike X-ray densitometry, it does not ionize the tissue. The strength of cancellous bone plays an essential role in the diagnosis of osteoporosis. The proposed work aims at developing mathematical tools for determining various parameters that describe the strength of porous-elastic materials, by probing the materials with mechanical waves such as ultrasound. The educational component emphasizes the interdisciplinary nature of the proposed research in several STEM fields. Through joint work with the PI's collaborators in mechanical and biomedical engineering, facilitated by the Center for Biomedical Engineering Research at the University of Delaware, a new interdisciplinary educational initiative linking biomedical engineering and mathematics for undergraduate and graduate student training is planned. The results from this project will be of interest to researchers who conduct laboratory experiments to study the relation between bone strength and bone micro-architecture and will open an avenue for more accurate and reliable ultrasound devices for measuring properties of porous-elastic materials.

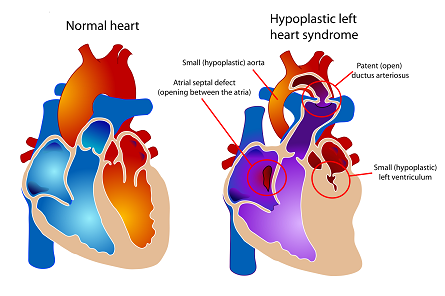
Hypoplastic left heart syndrome is a cardiac birth defect with a 20% mortality rate in the first year of life. Understanding the physiology of a patient in real time in the hospital is difficult. We are using mathematical models of the heart and circulatory system and selecting the parameters of the model based on continuously collected bedside vital signs. Our goal is to provide clinicians with patient-specific warnings and diagnostics.

This group develops mathematical models for tear film dynamics in close collaboration with optometrists' experiments to better understand various aspects of the tear film. Every time you blink, your upper lid paints on a thin multilayered fluid film that protects the ocular surface and helps you to see clearly. When the tear film doesn't have enough water, evaporates too quickly, or has other issues, the normal function may be compromised and lead to conditions such as "dry eye" that affect millions of people. Our models help ocular scientists understand the tear film in both health and disease. For a more detailed overview of the family of projects that we have studied, please see the project site.

When studying the processes underpinning disease and other biological systems, biochemists often need accurate estimates of reaction rates. Optical biosensors are a popular way to measure such reactions, as they do not disturb the underlying system. Correctly interpreting biosensor data requires having an accurate mathematical model for the system. Dr. Edwards has been working on models for these biosensors for over 15 years, focusing in particular on the BIAcore biosensor. The models involve partial differential equations that take into account not only the reactions, but also the transport in the biosensor. The PDE can often be reduced to an ordinary integrodifferential equation in experimentally relevant regimes.

Since surface plasmon resonance (SPR) and similar biosensors typically measure only mass changes, it can be difficult to analyze data from multiple simultaneous reactions. Current models do not work well when multiple reactions are occurring simultaneously. Areas of recent interest concern the formulation of a new model that will provide scientists a general roadmap on how to design experiments to analyze multiple reactions that occur at the same time (either crosslinked reactions or multicomponent reactions). A current area of biological interest is the study of translesion DNA synthesis, which is essential for cells to cope with DNA damage.

More information can be found at Prof. Cioaba's research page.

Our current research combines more than three decades of expertise in biotechnology, artificial intelligence and mathematical modeling, and is focussed on Mathematical and Computational Systems Biology and Systems Medicine. This research has resulted in over a hundred publications that have been cited 2500 times. We are applying mathematical models and knowledge-based artificial-intelligence approaches to convert data into useful knowledge. We build Physiology-based Pharmaco-kinetic (PBPK) models to understands how pharmaceutical molecules distribute themselves in the human body. We have recently built a systems connectivity model the explains how critical gut microorganisms and biomolecules are connected together at the systems-level and how they affect the brain to cause autism. Currently, we are building models to understand the spatio-temporal changes in the microbial composition of the gut and how these changes create imbalances that influence health and disease. The eventual goal of our modeling work is to be able to diagnose and predict diseases before they happen and to come up with therapies to prevent diseases via nutritional and proboitoic interventions. More information can be found at Prof. Dhurjati's research page.